Introduction

Let’s dive into the world of simple linear regression, a fundamental statistical technique used to model the relationship between two quantitative variables.

The Problem

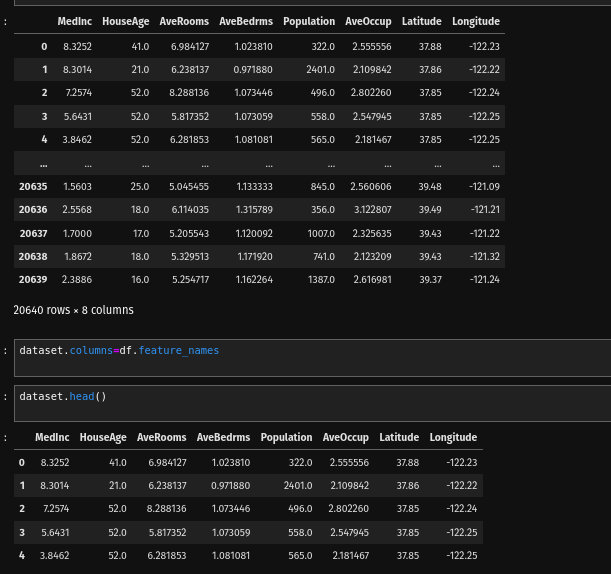
Our goal is to predict housing prices in California based on various factors such as location, median income, housing density, and more. By understanding the relationship between these variables and housing prices, we can provide valuable insights to stakeholders in the real estate industry.

dataset

Explore the Data

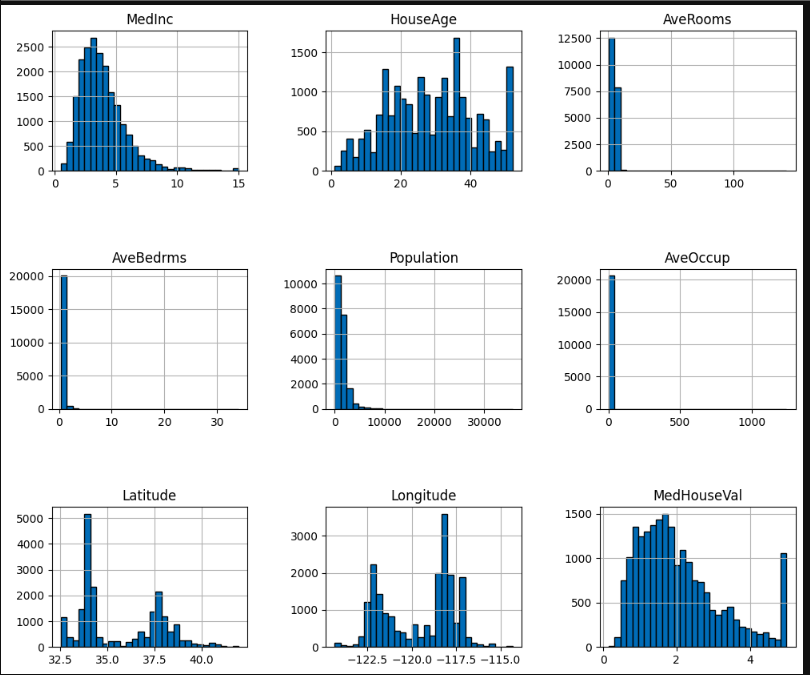
Perform exploratory data analysis (EDA) to gain insights into the dataset. Visualize key variables using scatter plots, histograms, and correlation matrices to understand their distributions and relationships. data data data

Train the model

regression = LinearRegression()
regression.fit(X_train,y_train)

Here we are fitting the model using Linear Regression

Evaluate the model

We evaluate the performance of the model using metrics such as Mean Squared Error (MSE) and Ridge Regressor

mse = cross_val_score(regression,X_train,y_train,scoring="neg_mean_squared_error", cv = 10)

ridgecv = GridSearchCV(ridge_regressor,parameters,scoring = 'neg_mean_squared_error', cv = 5)

Make Prediction

Now we predict the result using

reg_pred = regression.predict(X_test)

ridge_pred = ridgecv.predict(X_test)

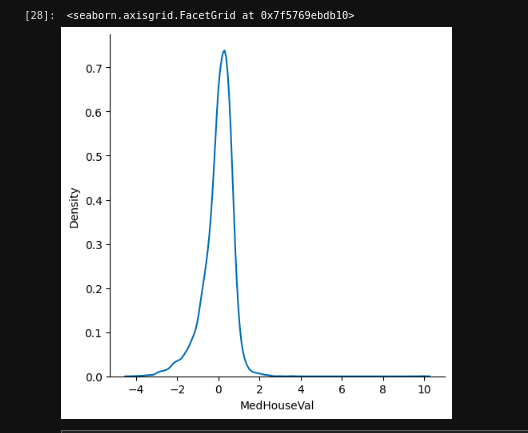
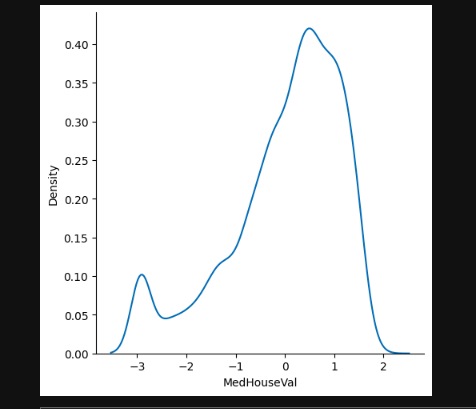
Visualize the data

We visualize the data using seaborn, displt function graph graph graph